Quote:
Originally posted by Hank Chinaski
This still doesn't make sense. If you're wrong Monty is forced to pick the other wrong door, whereas if you're right he can choose between two wrong doors. that's all the wheel says, isn't it?
|
I still don't get it either. For those too lazy to click over, here is the explanation:
"To analyze this problem we represent this senario as a random variable on a roulette wheel. The roulette wheel on the left simulates the Let's Make a Deal game. The inner wheel represents the number of the door that the car is behind, the middle wheel represents the door that is selected by the contestant, and the outer wheel represents the door Monty Hall can show. Spinning this roulette wheel once is equivalent to playing the game once. The outer wheel also tells you what your strategy should be to win. The red means that in order to win the contestant needs to switch doors, and the blue means that the contestant should not switch. Notice that there are twice as many red sections as blue. In other words, you are twice as likely to win if you switch than if you don't switch! What this wheel makes evident is that with probability 1/3 the contestant selects the correct door in which case it would be better not to switch. In the other 2/3 of the cases, Monty Hall is telling the contestant where the car is!"
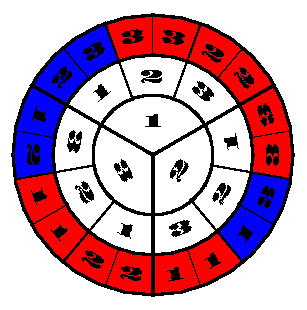
How is this an explanation?: "Notice that there are twice as many red sections as blue. In other words, you are twice as likely to win if you switch than if you don't switch!"
Anyone? Anyone?
TM

